Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. приемников электрической энергии.
Определение соединения сопротивлений треугольником
Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.
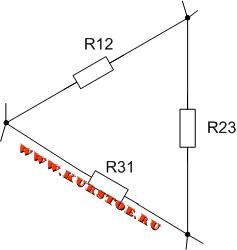
Соединение, при котором три сопротивления, находящиеся в пассивных ветвях, соединены между собою попарно и образуют замкнутый контур — называется треугольником.
Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.
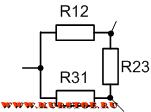
Определение соединения сопротивлений звездой
Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.
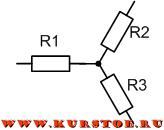
Причина преобразования треугольника в звезду
При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.

Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.
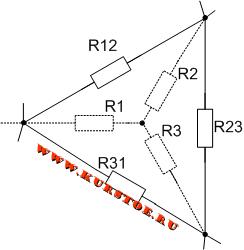
Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.

Формулы для расчета преобразования треугольника в звезду
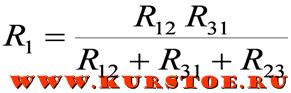
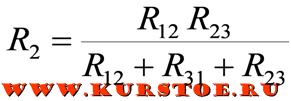
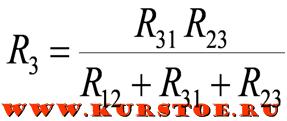
Пример преобразования
Для электрической цепи необходимо выполнить преобразование треуголькника R12 — R23 — R31 в звезду.
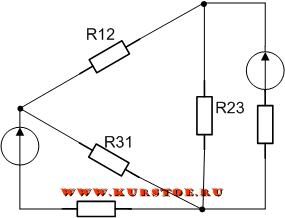
Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.
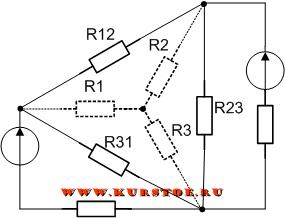
Удаляем соединение сопротивлений треугольником. В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.
Пусть требуется рассчитать цепь, показанную на рис. 7.1, а.

Рис. 7.1 — Преобразования электрической цепи
Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.
Треугольник и звезда сопротивлений имеют вид, показанный на рис. 7.2.

Рис. 7.2 — Треугольник и звезда сопротивлений
Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.
Можно показать, что условием эквивалентности являются следующие уравнения:
а) при преобразовании треугольника в звезду:

б) при преобразовании звузды в треугольник:

Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.
При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R3.
Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.
а) Решение преобразованием треугольника в звезду.

Теперь общее сопротивление цепи легко находится:

Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен:

Токи в паралельных ветвях:

Возвращаемся к исходной схеме (рис. 7.1, а):

Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A. Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.
б) Решение преобразованием звезды в треугольник.
Преобразуем звезду, образуемую в схеме на рис. 7.1, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 7.1, в).
Определяем сопротивления треугольника:

Теперь рассчитываем преобразованную цепь. Сначала находим эквивалентные сопротивления участков ac и cd:

Затем определяем общее сопротивление и токи:

Возвращаемся к исходной схеме:

Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.


| Главная // .. // § 2.23. Преобразование звезды в треугольник и треугольника в звезду |
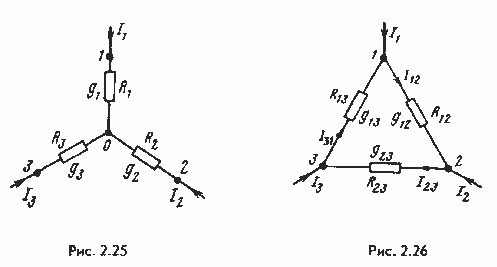
§ 2.23.Преобразование звезды в треугольник и треугольника в звезду. Соединение трех сопротивлений, имеющее вид трехлучевой звезды (рис. 2.25), называют звездой, а соединение трех сопротивлений так, что они образуют собой стороны треугольника (рис. 2.26), — треугольником. В узлах 1, 2, 3 (потенциалы их Φ1, Φ2 и Φ3) треугольник и звезда соединяются с остальной частью схемы (не показанной на рисунках).
Обозначим токи, подтекающие к узлам 1, 2, 3, через I1, I2 и I3.
Часто при подсчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовывать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема «не заметит» произведенной замены. Выведем формулы преобразований. С этой целью выразим токи I1, I2 и I33 в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.
Для звезды
 |
 |
Приборы для анализа качества электроэнергии
Подставим (2.24) в (2.23) и найдем Φ:
Введм Φ в выражение (2.24) для тока I1:
Для треугольника в соответствии с обозначениями на рис. 2.26
Так как ток I1, в схеме рис. 2.25 равен току I1 в схеме рис. 2.26 при любых значениях потенциалов Φ1Φ2Φ3, то коэффициент при Φ2 в правой части (2.27) равен коэффициенту при Φ2 в правой части (2.26), а коэффициент при Φ3 в правой части (2.27) — коэффициенту при Φ3 в правой части (2.26).
Следовательно
Формулы (2.28) — (2.30) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды. Они имеют легко запоминающуюся структуру: индексы у проводимостей в числителе правой части соответствуют индексам у проводимости в левой части; в знаменателе — сумма проводимостей лучей звезды.
Из уравнений (2.28) — (2.30) выразим сопротивления лучей звезды через сопротивления сторон треугольника:
С этой целью запишем дроби, обратыне (2.28)-(2.30):
Подставив (2.31),(2.33) и (2.34) в (2.32), получим
следовательно,
Подставив m в (2.33), найдем
Структура формул (2.35) — (2.37) аналогична структуре формул (2.28) — (2.30).
Преобразование треугольника в звезду можно пояснить, рас-смотрев, например, схему рис. 2.27, а, б. На рис. 2.27, а изображена схема до преобразования, пунктиром обведен преобразуемый треугольник. На рис. 2.27, б представлена та же схема после преобра-зования. Расчет токов произвести для нее проще (например, методом двух узлов), чем для схемы рис. 2.27, а.
В полезности преобразования звезды в треугольник можно убедиться на примере схем рис. 2.27, в, г. На рис. 2.27, в изображена схема до преобразования, пунктиром обведена преобразуемая в треугольник звезда. На рис. 2.27, г представлена схема после преобразования, которая свелась к последовательному соединению сопротивлений 1 .
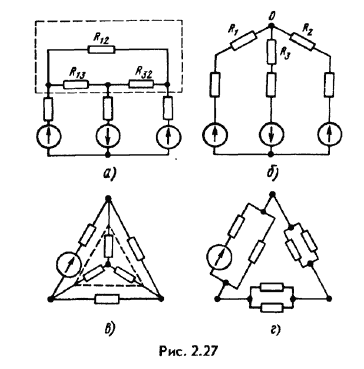 |
Пример 24. Найти значение сопротивлений R1,R2,R3 в схеме рис. 2.27, б, если сопротивления R12, R13, R13 в схеме рис. 2.27, a равны соответственно 2,3,5 Ом.
Решение По формуле (2.35),