Время переходного процесса формула

Время переходного процесса определяется как время, в течение которого переходная составляющая затухает до величины 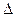% от своего начального значения. Поэтому для оценки времени переходного процесса необходимо рассмотреть скорость затухания мод системы.

Выражение (87) 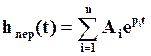включает в себя как апериодические составляющие (моды) 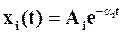, соответствующие вещественным полюсам , так и колебательные составляющие (моды) , соответствующие комплексно-сопряженным полюсам 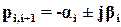. Затухание этих составляющих определяется множителем 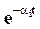. При этом чем больше вещественная часть 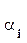полюса р_i(или сам вещественный полюс), тем быстрее затухает мода.

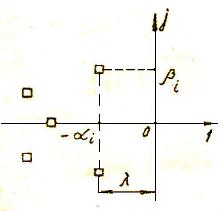
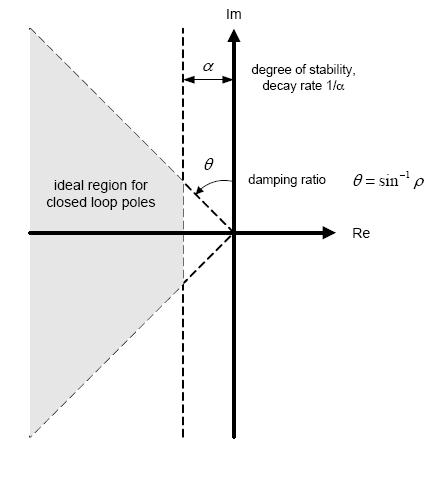
Корни характеристического уравнения (полюса замкнутой системы) удобно изображать в виде точек на комплексной плоскости (рис. 19), по осям которой отложены вещественная и мнимая части корней. Так как можно говорить только о качестве переходного процесса устойчивой системы, у которой вещественные части всех корней отрицательны, то все корни будут расположены слева от мнимой оси. При этом, чем дальше от мнимой оси расположены корни и 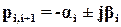, тем большему значению 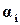они соответствуют.

Наиболее медленно будет затухать мода 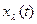, имеющая наименьшее 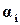. Поэтому можно приближенно считать, что скорость затухания переходного процесса определяется такой модой 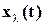, которая соответствует корням наиболее близко расположенным к мнимой оси. Величина 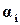, наименьшая из всех значений 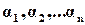, являющихся вещественными частями корней характеристического уравнения Д(р)=0, называется степенью устойчивости и обозначается 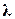(рис. 19).

Эта величина позволяет приближенно оценить время переходного процесса при 5% -допустимой ошибке

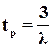. (89)

Оценка перерегулирования.

Перерегулирование системы зависит от поведения колебательных составляющих

,

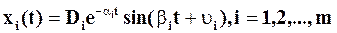так как колебательные процессы в системе будут наблюдаться только в том случае, когда характеристическое уравнение содержит комплексно-сопряженные корни 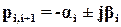. Склонность системы к колебаниям характеризует оценка

,

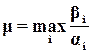которую называют колебательностью или степенью колебательности.

Таким образом, чем больше величина 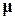, тем более колебательный характер будут иметь переходные процессы и наоборот. В пределе при 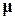=∞ полюса системы будут «чисто» мнимыми, и в ней будут наблюдаться переходные процессы в виде незатухающих колебаний. В случае, когда 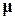=0, все корни характеристического уравнения будут вещественными, и в системе будут возникать апериодические процессы. Для системы второго порядка установлена взаимосвязь между колебательностью и перерегулированием в виде соотношения

.

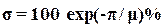Отметим, что при 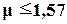значение перерегулирования в системе составит .

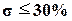Связь колебательности и относительного коэффициента затухания для системы второго порядка определяется формулой

.

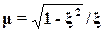Рассмотренные корневые методы оценки не учитывают влияние на постоянные коэффициенты А_i других нулей и полюсов замкнутой системы, наличие которых, как это видно из выражений (87) и (87а), может существенно изменить качество переходного процесса.

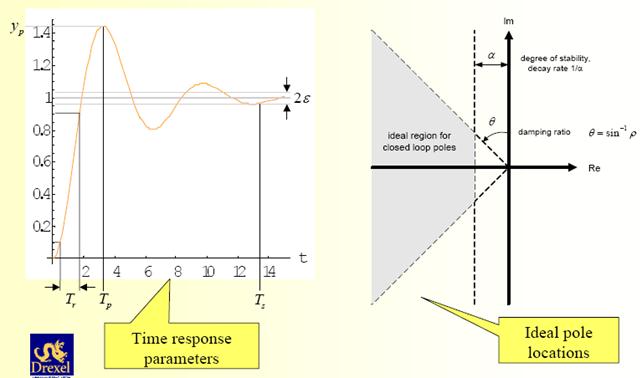
Анализируя выражения (87) и (87а), можно сделать следующие выводы относительно влияния расположения нулей и полюсов на вид и характер переходной характеристики.

1) Основное влияние на качество переходного процесса оказывает группа ближайших к мнимой оси нулей и полюсов (так называемых доминирующих нулей и полюсов).

2) Длительность переходного процесса в основном определяется степенью устойчивости системы, равной абсолютному значению вещественной части ближайших к мнимой оси комплексных полюсов замкнутой системы или вещественного полюса, если он является ближайшим к мнимой оси. При этом длительность переходного процесса может быть определена по формуле (89) .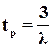

3) Величина перерегулирования 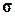зависит от степени колебательности 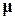доминирующих комплексных полюсов и от степени близости к мнимой оси остальных нулей и полюсов замкнутой системы.

4) Близкие к мнимой оси нули увеличивают перерегулирование, а близкие (но не доминирующие) полюсы его уменьшают.

Не останавливаясь на доказательстве всех этих пунктов, приведем лишь соображения, подтверждающие вывод об увеличении перерегулирования при введении в систему нулей.

Пусть САУ описывается в отсутствии нулей передаточной функцией Ф(р). Введем в эту систему левый нуль z= —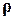, так чтобы при этом не изменился коэффициент усиления замкнутой системы k_з=Ф(0). Тогда передаточная функция примет вид

.

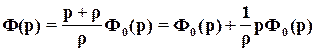найдем переходную характеристику полученной системы

,

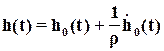как сумму переходной характеристики 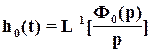исходной и взвешенной производной этой характеристики.

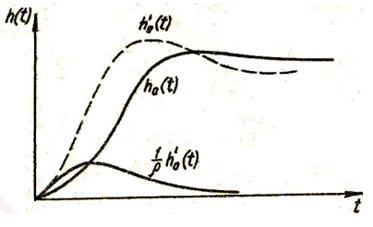
В начале переходного процесса характеристика h(t) возрастает с большой скоростью и поэтому ее производная 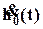положительна и имеет большую величину (рис. 24). В результате сложения кривых h(t) и 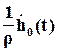получается кривая h(t), имеющая большее перерегулирование, причем перерегулирование увеличивается тем значительнее, чем меньше абсолютное значение 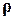нуля передаточной функции Ф(р).

Введение большего числа нулей приводит к тому же эффекту.

Для системы второго порядка с комплексно-сопряженными полюсами с ПФ

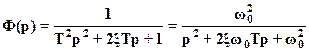
введение левого нуля z= —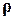увеличивает перерегулирование при а=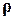

|	следующая лекция ==>
Корневые методы оценки качества переходного процесса	|	Чувствительность систем управления к изменению параметров

Дата добавления: 2014-01-07 ; Просмотров: 3074 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Рассмотрим переходные процессы в цепи, содержащей последовательно соединенные резистор R и индуктивность L . Уравнение Кирхгофа для такой цепи

где u = u ( t ) — напряжение на входе цепи. Найдем решение этого уравнения для свободной составляющей тока, т.е. при u = 0, в виде i с = I e pt . Для этого подставим выражение для тока в исходное уравнение и найдем значение p

Выражение Lp + R =0 представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных тока на p k , где k — порядок производной.

Таким образом, общее решение для тока при переходном процессе в R-L цепи можно представить в виде

где t = 1/|p| = L / R — постоянная времени переходного процесса; I — постоянная интегрирования, определяемая по начальным значениям; i — установившийся ток в цепи, определяемый по параметрам R и L и напряжению на входе u .

Длительность переходного процесса в цепи, определяемая значением t , возрастает с увеличением L и уменьшением R .

Рассмотрим подключение R — L цепи к источнику постоянной ЭДС E (рис. 1 а)).

Установившийся ток в этой цепи будет определяться только ЭДС E и резистивным сопротивлением R , т.к. после окончания переходного процесса i = const и u L = Ldi / dt = 0, т.е. i у = E / R .

Полный ток в переходном процессе из выражения (1)

Для определения постоянной I найдем начальное тока. До замыкания ключа ток очевидно был нулевым, а т.к. подключаемая цепь содержит индуктивность, ток в которой не может измениться скачкообразно, то в первый момент после коммутации ток останется нулевым. Отсюда

Подставляя найденное значение постоянной I в выражение для тока, получим

Из этого выражения можно определить падения напряжения на резисторе u R и индуктивности u L

Из выражений (1)-(3) следует, что ток в цепи нарастает по экспоненте с постоянной времени t = L / R от нулевого до значения E / R (рис. 1 б)). Падение напряжения на сопротивлении u R повторяет кривую тока в измененном масштабе. Напряжение на индуктивности u L в момент коммутации скачкообразно возрастает от нуля до E , а затем снижается до нуля по экспоненте (рис. 1 б)).

Подставляя выражения (3) в уравнение Кирхгофа для цепи после коммутации, можно убедиться в его справедливости в любой момент времени

Пусть рассмотренная выше R — L цепь длительное время была подключена к источнику ЭДС E , а затем замкнута накоротко (рис. 2 а)).

В этом случае установившийся ток будет равен нулю и задача сводится к отысканию его свободной составляющей. Из выражения (1)

Постоянную I можно определить из начальных условий. Установившийся ток в цепи до переключения ключа S был равен i (0 — ) = E / R , а т.к. в первый момент после коммутации ток в индуктивности сохраняет свое значение, то i (0 — ) = i (0 + ) = I = E / R . Отсюда ток и падения напряжения в цепи

Из выражений (4) следует, что при замыкании цепи накоротко ток уменьшается от E / R до нуля по экспоненте с постоянной времени t = L / R (рис. 2 б)). Падение напряжения на резисторе изменяется по такому же закону, а напряжение на индуктивности в момент коммутации скачком изменяется от нуля до — E , а затем снижается до нуля ( рис. 2б)).

Общее падение напряжения на резисторе и индуктивности в любой момент времени

как и следовало ожидать, равно нулю и в переходном процессе происходит преобразование энергии магнитного поля в тепло.

При отключении цепи содержащей индуктивность в ней могут возникать падения напряжений опасные для ее элементов. Пусть R — L цепь с подключенным к ней вольтметром отключается от источника постоянной ЭДС E (рис. 3).

Так как цепь содержит индуктивность, то после размыкания ключа S ток не сможет изменить своего значения и будет протекать в контуре R — L — V . Значение тока до коммутации i (0 — ) = E / R = i (0 + ) = i (0) Уравнение Кирхгофа для этого контура

Ri + R V i + u L = 0,

где R V — сопротивление вольтметра.

Отсюда падение напряжения на вольтметре u V = R V i (0) = ER V / R и на индуктивности u V = ( R + R V ) i (0) = E (1+ R V / R ).

Обычно R V >> R , поэтому напряжение на вольтметре и на индуктивности в момент отключения превосходят ЭДС источника в R V / R раз. Это может быть опасным для вольтметра и изоляции катушки. Если индуктивность цепи достаточно велика, то запасенной в ней энергии может оказаться достаточно для разрушения изоляции или входных цепей прибора. Поэтому при отключении цепи постоянного тока с большой индуктивностью ее предварительно замыкают на малое сопротивление, а измерительные приборы отключают .

Рассмотрим теперь процесс подключения R — L цепи к источнику переменной синусоидальной ЭДС (рис. 4 а)).

Ток после коммутации в соответствии с выражением (1)

Установившееся значение i у определяется по закону Ома как

где y — фаза напряжения на входе цепи в момент коммутации, а j = arctg( w L / R ) .

До коммутации ток в цепи был равен нулю, поэтому из выражений (5) и (6) можно найти постоянную I

следовательно, полный ток в цепи после коммутации

Таким образом, ток в цепи состоит из двух составляющих — установившегося периодического синусоидального тока и свободного, уменьшающегося по экспоненте с постоянной времени t = L / R (рис. 4 б)). В результате, ток в некоторые моменты времени превышает амплитудное значение установившегося тока.

Начальное значение свободной составляющей тока I m sin( y — j ) зависит от момента включения y . При y = j +( k +1/2) p ( k = 0, 1, 2 ј ) ток через полпериода после коммутации (рис. 4 в)) достигает максимального значения, равного I max = I m [1+e — p t /( w t ) ]. Значение e — p t /( w t ) w и постоянной времени t . При w ® µ и/или t ® µ I max ® 2.

При y = j + k p ( k = 0, 1, 2 ј ) свободный ток в момент коммутации равен нулю и переходный процесс отсутствует . В цепи сразу после коммутации возникает установившийся режим. Эта особенность переходных процессов на переменном токе используется в устройствах детерминированного включения . В них момент включения нагрузки выбирают таким образом, чтобы уменьшить или исключить большие значения тока, напряжения или других параметров.

Перейдем к рассмотрению переходных процессов в цепи с последовательным соединением резистора R и емкости C . По второму закону Кирхгофа для этой цепи

Ток в емкости можно представить в виде i = Cdu C / dt . Отсюда

Решение этого дифференциального уравнения для напряжения на емкости также можно представить суммой свободной и установившейся составляющих u C = u у + u с . Свободную составляющую найдем из решения однородного уравнения ( u = 0) в виде u с = U e pt . Подставим это выражение в уравнение и найдем значение p

Выражение RCp + 1 = 0 представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных от напряжения на емкости на p k , где k — порядок производной.

Отсюда общее решение для напряжения на емкости

u C = u у + u с = u у + U e — t / t ,

где U — постоянная интегрирования, определяемая из начальных значений; t = 1/|p| = RC — постоянная времени переходного процесса.

Рассмотрим процесс подключения последовательной R — C цепи к источнику постоянной ЭДС E (рис. 5 а)).

В отличие от индуктивности, емкость после накопления заряда может длительное время сохранять его. Поэтому начальное значение напряжения на емкости U 0 может быть произвольным и иметь произвольный знак по отношению к ЭДС источника.

Установившееся значение напряжения на емкости после замыкания ключа S всегда будет равно E , т.к. на постоянном токе в установившемся режиме du C / dt = 0 и i = Cdu C / dt = 0, а u C = u — Ri = E — Ri = E . Поэтому из выражения (8) напряжение на емкости в общем виде будет равно

u C = u у + u с = E + U e — t / t .

Пусть напряжение на емкости до коммутации было u C (0 — ) = ± U 0 (знак + соответствует полярности напряжения на рис. 5 а) без скобок). Тогда из (9) для момента времени непосредственно после замыкания ключа найдем постоянную U

а затем и выражение для напряжения на емкости в виде

где t = RC — постоянная времени переходного процесса.

Отсюда можно найти ток в цепи и падение напряжения на резисторе

На рис. 5 б)-г) приведены временные диаграммы переходного процесса подключения R — C цепи к источнику постоянной ЭДС для трех вариантов начальных значений напряжения на емкости: 1) E > U 0 > 0 ; 2) E U 0 и U 0 > 0; 3) U 0 U 0 до E . В то время как ток и напряжение на резисторе в момент коммутации скачкообразно изменяются на величину пропорциональную разности или сумме E и U 0 , а затем монотонно уменьшаются до нуля. При этом, если E U 0 , то ток и падение напряжения на R отрицательны, т.е. происходит разряд емкости.

Полный разряд емкости происходит при отсутствии внешних источников энергии (рис. 1 а)). После переключения ключа S вся энергия накопленная в электрическом поле емкости C преобразуется в тепло в резисторе R .

Напряжение на емкости в переходном процессе будет иметь только свободную составляющую

u C = u с = U e — t / t

и если цепь достаточно длительное время была подключена к источнику, то в момент переключения напряжение на емкости будет равно E . Поэтому постоянная U будет равна

u C (0 — ) = E = u C (0 + ) = U ,

а напряжение на емкости в переходном процессе —

u C = E e — t / t .

Отсюда ток в цепи и напряжение на резисторе

К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.

Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).

Классификация показателей качества состоит из нескольких групп:

• прямые — определяемые непосредственно по переходной характеристике процесса,
• корневые — определяемые по корням характеристического полинома,
• частотные — по частотным характеристикам,
• интегральные — получаемые путем интегрирования функций.

Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:

1. Установившееся значение выходной величины Yуст,
2. Степень затухания ?,
3. Время достижения первого максимума tmax,
4. Время регулированияtp,
5. Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
6. Перерегулированиеу,
7. Динамический коэффициент регулирования Rd,
8. Показатель колебательностиМ.

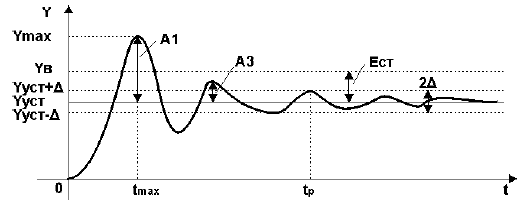
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.

Рисунок 1 — Определение показателей качества по переходной характеристике

Установившееся значение выходной величины Yуст

Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.

Степень затухания ?

Степень затухания ? определяется по формуле:

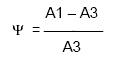
где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.

Время достижения первого максимума tmax

Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.

Время регулирования tp

Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.

В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.

Ошибка регулирования Ест

Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.

Перерегулирование у

Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:

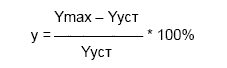
где значения величин Ymax и Yуст определяются согласно рис.1.

При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:

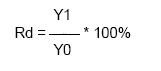
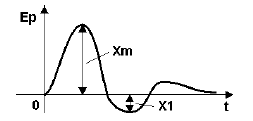
где значения величин Xm и X1 определяются согласно рис. 2.

Рисунок 2 — График переходного процесса при отработке возмущения

Динамический коэффициент регулирования Rd

Динамический коэффициент регулирования Rd определяется из формулы:

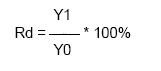
где значения величин Y1 и Y0 определяются согласно рис. 3.

Рисунок 3 — К понятию динамического коэффициента регулирования

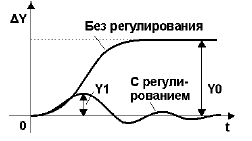
Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.

Показатель колебательности М

Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.

Рисунок 4 — График модуля частотной передаточной функции замкнутой системы

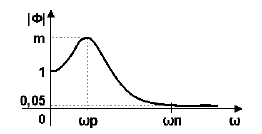
Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.

В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.