
Решение задач по гидравлике запись закреплена
Теплопроводность при стационарном режиме
1-1. Вычислить плотность теплового потока через плоскую однородную стенку, толщина которой значительно меньше ширины и высоты, если стенка выполнена: а) из стали [λ = 40 Вт/(м · ºС)]; б) из бетона [λ = 1,1 Вт/ (м · ºС)]; в)из диатомитового кирпича [λ = 0,11 Вт/(м · ºС)].
Во всех трех случаях толщина стенки δ = 50 мм. Температуры на поверхностях стенки поддерживаются постоянными:
tс1 = 100ºС и tс2 = 90ºС.
1-2. Плотность теплового потока через плоскую стенку толщиной δ = 50 мм q = 70 Вт/м2.
Определить разность температур на поверхностях стенки и численные значения градиента температуры в стенке, если она выполнена: а) из латуни [λ = 70 Вт/(м · ºС)]; б) из красного кирпича [λ = 0,7 Вт/(м · ºС)]; в) из пробки [λ = 0,07 Вт/(м · ºС)].
1-3. Определить потерю теплоты Q, Вт, через стенку из красного кирпича длиной l = 5 м, высотой h = 4 м и толщиной δ = 0,250 м, если температуры на поверхностях стенки поддерживаются tс1 = 110ºС и tс2 = 40ºС. Коэффициент теплопроводности красного кирпича λ = 0,70 Вт/(м · ºС).
1-4. Определить коэффициент теплопроводности материала стенки, если при толщине ее δ = 40 мм и разности температур на поверхностях Δt = 20ºС плотность теплового потока q = 145 Вт/м2.
1-5. Плоскую поверхность необходимо изолировать так, чтобы потери теплоты с единицы поверхности в единицу времени не превышали 450 Вт/м2. Температура поверхности под изоляцией tс1 = 450ºС, температура внешней поверхности изоляции tс2 = 50ºС.
Определить толщину изоляции для двух случаев:
а) изоляция выполнена из совелита, для которого
λ = 0,09 + 0,0000874 t;
б) изоляция выполнена из асботермита, для которого
λ = 0,109 + 0,000146 t.
1-6. Плоская стенка выполнена из шамотного кирпича толщиной δ = 250 мм. Температура ее поверхностей: tс1 = 1350°С и tс2 = 50°С. Коэффициент теплопроводности шамотного кирпича является функцией от температуры λ = 0,838 (1 + 0,0007 t).
Вычислить и изобразить в масштабе распределение температуры в стенке.
Тепловые потери q = 1090 Вт/м2. Температура в плоскости соприкосновения слоев tc2 = 828°С.
1-7. Температуры на поверхностях шамотной стенки, толщина которой δ = 200 мм, равны: tс1 = 1000ºС и tс2 = 200ºС. Коэффициент теплопроводности шамота изменяется в зависимости от температуры по уравнению λ = 0,813 + 0,000582 t.
Показать, что плотность теплового потока q, Вт/м2, в случае линейной зависимости коэффициента теплопроводности от температуры может быть вычислена по формуле для постоянного коэффициента теплопроводности, взятого при средней температуре стенки.
Найти ошибку в определении температуры в точках х = 57,5; 110 и 157,5 мм, если вычисления производятся по значению коэффициента теплопроводности, среднему для заданного интервала температур, и построить график распределения температуры в стенке.
1-8. Плоская стенка бака площадью F = 5 м2 покрыта двухслойной тепловой изоляцией. Стенка бака стальная, толщиной δ1 = 8 мм, с коэффициентом теплопроводности λ1 = 46,5 Вт/(м · ºС). Первый слой изоляции выполнен из новоасбозурита толщиной δ2 = 50 мм, коэффициент теплопроводности которого определяется уравнением
λ2 = 0,144 + 0,00014 t.
второй слой изоляции толщиной δ3 = 10 мм представляет собой штукатурку (известковую), коэффициент теплопроводности которой λ3 = 0,698 Вт/(м · ºС).
Температуры внутренней поверхности стенки бака tс1 = 250ºС и внешней поверхности изоляции tс2 = 50ºС.
Вычислить количество теплоты, передаваемой через стенку, температуры на границах слоев изоляции и построить график распределения температуры.
1-9. Обмуровка печи состоит из слоев шамотного и красного кирпича, между которыми расположена засыпка из диатомита (рис. 1-3). Толщина шамотного слоя δ1 = 120 мм, диатомитовой засыпки δ2 = 50 мм и красного кирпича δ3 = 250 мм. Коэффициенты теплопроводности материалов соответственно равны:
λ1 = 0,93; λ2 = 0,13 и λ3 = 0,7 Вт/(м · ºС).
1-10. Стенка неэкранированной топочной камеры парового котла выполнена из слоя пеношамота толщиной δ1 = 125 мм и слоя красного кирпича толщиной δ2 = 500 мм. слои плотно прилегают друг к другу. Температура на внутренней поверхности топочной камеры tс1 = 1100ºС, а на наружной tс3 = 50ºС (рис. 1-4). Коэффициент теплопроводности пеношамота λ1 = 0,28 + 0,00023 t, красного кирпича λ2 = 0,7 Вт/(м · ºС).
Вычислить тепловые потери через 1 м2 стенки топочной камеры и температуру в плоскости соприкосновения слоев.
1-11. Толщину слоя красного кирпича в стенке топочной камеры, рассмотренной в задаче 1-10, решено уменьшить в 2 раза, а между слоями поместить слой засыпки из диатомитовой крошки (рис. 1-5), коэффициент теплопроводности которой
λ = 0,113 + 0,00023 t.
Какую нужно сделать толщину диатомитовой засыпки, чтобы при тех же температурах на внешних поверхностях стенки, что и в задаче 1-10, потери теплоты оставались неизменными?
1-12. Стены сушильной камеры выполнены из слоя красного кирпича толщиной δ1 = 250 мм и слоя строительного войлока. Температура на внешней поверхности кирпичного слоя tс1 = 110ºС и на внешней поверхности войлочной слоя tс3 = 25ºС.
Коэффициент теплопроводности красного кирпича λ1 = 0,7 Вт/(м · ºС) и строительного войлока λ2 = 0,0465 Вт/(м · ºС).
Вычислить температуру в плоскости соприкосновения слоев и толщину войлочного слоя при условии, что тепловые потери через 1 м2 стенки камеры не превышают q = 110 Вт/м2.
1-13. В приборе для определения коэффициента теплопроводности материалов между горячей и холодной поверхностями расположен образец из испытуемого материала (рис. 1-6).
Образец представляет собой диск диаметром d = 120 мм и толщиной δ = 20 мм.
Температура горячей поверхности tс1 = 180ºС, холодной tс2 = 30ºС. Тепловой поток через образец после установления стационарного процесса Q = 50,6 Вт. Благодаря защитным нагревателям радиальные потоки теплоты отсутствуют.
Вследствие плохой пригонки между холодной и горячей поверхностями и образцом образовались воздушные зазоры толщиной δв = 0,1 мм. Вычислить относительную ошибку в определении коэффициента теплопроводности Δλ, если при обработке результатов измерений не учитывать образовавшихся зазоров. Коэффициент теплопроводности воздуха в зазорах отнести к температурам соответствующих поверхностей tс1 и tс2.
1-14. Вычислить потери теплоты через единицу поверхности кирпичной обмуровки парового котла в зоне размещения водяного экономайзера и температуры на поверхностях стенки, если толщина стенки δ = 250 мм, температура газов tж1 = 700ºС и воздуха в котельной tж2 = 30ºС. Коэффициент теплоотдачи от газов к поверхности стенки α1 = 23 Вт/(м2 · ºС) и от стенки к воздуху α2 = 12 Вт/(м2 · ºС). Коэффициент теплопроводности стенки λ = 0,7 Вт/(м · ºС).
1-15. Вычислить тепловой поток через 1 м2 чистой поверхности нагрева парового котла и температуры на поверхностях стенки, если заданы следующие величины: температура дымовых газов tж1 = 1000ºС, кипящей воды tж2 = 200ºС; коэффициенты теплоотдачи от газов к стенке α1 = 100 Вт/(м2 · ºС) и от стенки к кипящей воде α2 = 5000 Вт/(м2 · ºС).
Коэффициент теплопроводности материала стенки λ = 50 Вт/(м · ºС) и толщина стенки δ = 12 мм.
1-16. Решить задачу 1-15 при условии, что в процессе эксплуатации поверхность нагрева парового котла со стороны дымовых газов покрылась слоем сажи толщиной δс = 1 мм [λс = 0,08 Вт/(м · ºС)] и со стороны воды слоем накипи толщиной δп = 2 мм [λп = 0,8 Вт/(м · ºС)].
Вычислить плотность теплового потока через 1 м2 загрязненной поверхности нагрева и температуры на поверхностях соответствующих слоев tс1, tс2, tс3 и tс4 (рис. 1-8). Сравнить результаты расчета с ответом задачи 1-15 и определить уменьшение тепловой нагрузки.
1-17. Определить тепловой поток через 1 м2 кирпичной стены помещения толщиной в два кирпича (δ = 510 мм) с коэффициентом теплопроводности λ = 0,8 Вт/(м · ºС). Температура воздуха внутри помещения tж1 = 18ºС; коэффициент теплоотдачи к внутренней поверхности стенки α1 = 7,5 Вт/(м2 · ºС); температура наружного воздуха tж2 = — 30ºС; коэффициент теплоотдачи от наружной поверхности стены, обдуваемой ветром, α2 = 20 Вт/(м2 · ºС). Вычислить также температуры на поверхностях стены tс1 и tс2.
1-18. Решить задачу 1-17, если стена покрыта снаружи слоем тепловой изоляции толщиной 50 мм с коэффициентом теплопроводности λиз = 0,08 Вт/(м · ºС). Сравнить потери теплоты через изолированную и неизолированную стенки.
1-19. Вычислить плотность теплового потока q, Вт/м2, в пластинчатом воздухоподогревателе и значения температур на поверхностях листов, если известно, что средняя температура газов tж1 = 315ºС и средняя температура воздуха tж2 = 135ºС, соответственно коэффициенты теплоотдачи α1 = 23 Вт/(м2 · ºС) и α2 = 30 Вт/(м2 · ºС). Толщина листов подогревателя δ = 2 мм. Коэффициент теплопроводности материала листов λ = 50 Вт/(м · ºС).
1-20. Обмуровка печи выполнена из слоя шамотного кирпича с коэффициентом теплопроводности λ = 0,84 (1 + 0,695 · 10-3 t) Вт/(м · °С); толщина обмуровки δ = 250 мм.
Определить потери теплоты с одного квадратного метра поверхности q, Вт/м2, и температуры на внешних поверхностях стены, если температура газов в печи tж1 = 1200°С и воздуха в помещении tж2 = 30°С, коэффициент теплоотдачи от газов к стенке α1 = 30 Вт/(м2 × °С) и от обмуровки к окружающему воздуху α2 = 10 Вт/(м2 · °С).
1-21. В камере сгорания парового котла с жидким золоудалением температура газов должна поддерживаться равной tж1 = 1300ºС, температура воздуха в котельной tж2 = 30ºС. Стены топочной камеры выполнены из слоя огнеупора толщиной δ1 = 250 мм с коэффициентом теплопроводности λ1 = 0,28 (1 + 0,833 · 10-3 t) Вт/(м · ºС) и слоя диатомитового кирпича с коэффициентом теплопроводности λ2 = 0,113 (1 + 0,206 · 10-3 t) Вт/(м · ºС).
Коэффициент теплоотдачи от газов к обмуровке α1 = 30 Вт/(м2 · ºС) и от внешней поверхности топочной камеры к окружающему воздуху α2 = 10 Вт/(м2 · ºС).
Какой должна быть толщина диатомитового слоя, чтобы потери в окружающую среду не превышали 750 Вт/м2?
1-22. Змеевики пароперегревателя выполнены из труб жароупорной стали диаметром d1/d2 = 32/42 мм с коэффициентом теплопроводности λ = 14 Вт/(м · ºС). Температура внешней поверхности трубы tс2 = 580ºС и внутренней поверхности tс1 = 450ºС.
Вычислить удельный тепловой поток через стенку на единицу длины трубы q1, Вт/м.
1-23. Паропровод диаметром 150/160 мм покрыт слоем тепловой изоляции толщиной δиз = 100 мм; коэффициенты теплопроводности стенки трубы λ1 = 50 Вт/(м · ºС) и изоляции λ2 = 0,08 Вт/(м · ºС). Температура на внутренней поверхности паропровода tс1 = 400ºС и на наружной поверхности изоляции tс3 = 50ºС (рис. 1-9).
Найти тепловые потери с 1 м паропровода и температуру на границе соприкосновения паропровода и изоляции.
1-24. Стальной трубопровод диаметром d1/d2 = 100/110 мм с коэффициентом теплопроводности λ1 = 50 Вт/(м · ºС) покрыт изоляцией в два слоя одинаковой толщиной δ2 = δ3 = 50 мм. Температура внутренней поверхности трубы tс1 = 250ºС и наружной поверхности изоляцией tс4 = 50ºС (рис. 1-10).
Определить потери теплоты через изоляцию с 1 м трубопровода и температуру на границе соприкосновения слоев изоляции, если первый слой изоляции, накладываемый на поверхность трубы, выполнен из материала с коэффициентом теплопроводности λ2 = 0,06 Вт/(м · ºС), а второй слой – из материала с коэффициентом теплопроводности λ3 = 0,12 Вт/(м · ºС).
1-25. Как изменятся тепловые потери с 1 м трубопровода, рассмотренного в задаче 1-24, если слои изоляции поменять местами, т.е. слой с большим коэффициентом теплопроводности наложить непосредственно на поверхность трубы? Все другие условия оставить без изменений.
1-26. Паропровод диаметром d1/d2 = 160/170 мм покрыт слоем изоляции толщиной δ = 100 мм с коэффициентом теплопроводности, зависящим от температуры следующим образом: λиз = 0,062 (1 + 0,363 · 10-2 t).
Определить потери теплоты с 1 м паропровода и температуру на внутренней поверхности трубопровода, если температура наружной поверхности трубы tс2 = 300ºС, а температура внешней поверхности изоляции не должна превышать 50ºС.
1-27. Железобетонная дымовая труба (рис. 1-11) внутренним диаметром d2 = 800 мм и наружным диаметром d3 = 1300 мм должна быть футерована внутри огнеупором.
Определить толщину футеровки и температуру наружной поверхности трубы tс3 из условий, чтобы тепловые потери с 1 м трубы не превышали 2000 Вт/м, а температура внутренней поверхности железобетонной стенки tс2 не превышала 200ºС. Температура внутренней поверхности футеровки tс1 = 425ºС; коэффициент теплопроводности футеровки λ1 = 0,5 Вт/(м · ºС); коэффициент теплопроводности бетона λ2 = 1,1 Вт/(м · ºС).
1-28. В условиях задачи 1-27 определить толщину футеровки δ, если она выполнена из шамотного кирпича. Расчет произвести с учетом зависимости коэффициента λ от температуры по формуле λ = 0,84 + 0,0006 t.
1-29. В приборе для определения коэффициента теплопроводности жидкостей по методу «нагретой нити» (рис. 1-12) в кольцевой зазор между платиновой нитью и кварцевой трубкой залито испытуемое трансформаторное масло. Диаметр и длина платиновой нити d1 = 0,12 мм и l = 90 мм; внутренний и наружный диаметры кварцевой трубки d2 = 1 мм и d3 = мм; коэффициент теплопроводности кварца λ = 1,4 Вт/(м · ºС).
Вычислить коэффициент теплопроводности λж и среднюю температуру tж трансформаторного масла, если при расходе теплоты через кольцевой слой масла Q = 1,8 Вт, температура платиновой нити tс1 = 106,9ºС и температура внешней поверхности кварцевой трубки tс3 = 30,6ºС.
1-30. Вычислить допустимую силу тока для медного провода d = 2 мм, покрытого резиновой изоляцией толщиной δ = 1 мм, при условии, что максимальная температура изоляции должна быть не выше 60ºС, а на внешней поверхности изоляции 40ºС. Коэффициент теплопроводности резины λ = 0,15 Вт/(м · ºС). Электрическое сопротивление медного провода R = 0,005 Ом/м.
1-31. Определить площадь поверхности нагрева конвективного пароперегревателя, выполненного из труб жаростойкой стали диаметром d1/d2 = 32/40 мм. Коэффициент теплопроводности стали λ = 39,5 Вт/(м · ºС). Производительность пароперегревателя Q = 61,1 кг/с пара. В пароперегреватель поступает сухой насыщенный пар при давлении р = 9,8 МПа. Температура перегретого пара на выходе tн = 500ºС.
Коэффициент теплоотдачи от газов к стенке а2 = 81,5 Вт/(м2 · ºС), а от стенки к пару а1 = 1163 Вт/(м2 · ºС); средняя температура газов tж = 900ºС. Гидравлическим сопротивлением пароперегревателя пренебречь.
1-32. Решить задачу (1-31), пренебрегая кривизной стенки (как для плоской стенки). Полученную площадь поверхности нагрева сравнить с результатом, полученным в задаче 1-31.
РЕШЕНИЕ
| Дано | Решение |
| δ1=250 мм δ2=50 мм δ3=250 мм λ1=0,94 Вт/(м∙К) λ2= 0,13 Вт/(м∙К) λ3=0,7 Вт/(м∙К) | 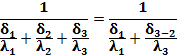 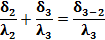  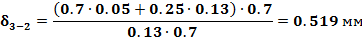 |
| δ3-2-? | |
Ответ: 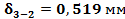 |
6.Стенка неэкранированной топочной камеры парового котла выполнена из слоя пеношамота толщиной δ1, мм и слоя красного кирпича толщиной δ2, мм. Слой плотно прилегают друг к другу. Температура на внутренней поверхности топочной камеры tс1, ºС, а на наружной tc3, ºС. Коэффициент теплопроводности пеношамота λ1=0,28+0,00023*t, а красного кирпича λ3, Вт/(м∙К). Вычислить тепловые потери через 1 м 2 стенки топочной камеры и температуры на плоскости соприкосновения слоев.
| δ1 | δ2 | tc1 | tc3 | λ1 | λ2 |
| 0,28+0,00023*t | 0,5 |
| Дано | |
| δ1=250 мм δ2=125 мм tc1=1000 ºС. tc3=60 ºС. λ1=0,28+0,00023*t λ3=0,50 Вт/(м∙К). | Определим сродную температуру, по формуле: 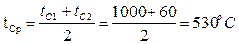 Определим коэффициент теплопроводности для новоасбозурита, по формуле: Определим коэффициент теплопроводности для новоасбозурита, по формуле: 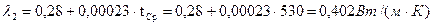 Определяем тепловой поток, по формуле: Определяем тепловой поток, по формуле: 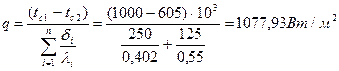 |
| q-? tC2-? | |
Определим температуру tC2 на границе слоев, по формулам: 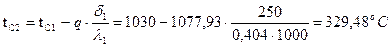 |
|
Ответ: 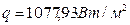 , , 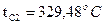 . . |
7.Стена сушильной камеры выполнены из слоя красного кирпича толщиной δ1, мм и слоя строительного войлока. Температура на внешней поверхности кирпичного слоя tс1, ºС и на внешней поверхности войлочного слоя tc3, ºС. Коэффициент теплопроводности красного кирпича λ1, Вт/(м∙К) и строительного войлока λ2, Вт/(м∙К). Вычислить температуру в плоскости соприкосновения слоев и толщину войлочного слоя при условии, что тепловые потери через 1 м 2 стенки не превышает q=110 Вт/м 2 .
Дата добавления: 2015-05-26 ; Просмотров: 10916 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Г л а в а п е р в а я . СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
ного кирпича [λ к = 0,71 Вт/(м æ К)] и слоя войлока [λ в = 0,047 Вт/(м æ К)], имели температуры t с1 = 120 °С и t с3 = 35 °C на внутренней и внешней поверхностях соответственно. Увеличение толщины слоя войлока на 0,028 м снизило тепловые потери вдвое и t с3 на 10 °С при неизменной t с1 . Определить толщину кирпичного слоя и максимальные температуры войлока в обоих случаях.
1.11. Обмуровка печи состоит из слоев шамотного кирпича [λ ш =
= 0,93 Вт/(м æ К), δ ш = 120 мм] и красного кирпича [λ к = 0,7 Вт/(м æ К), δ к = 250 мм], между которыми засыпка из диатомита [λ д = 0,13 Вт/(м æ К), δ д = 60 мм]. Какой толщины следует сделать слой засыпки, если тол-
щину слоя из красного кирпича удвоить при условии сохранения плотности теплового потока через обмуровку и температур на внешних ее поверхностях?
1.12. Плотность теплового потока через плоскую кварцевую
стенку [λ = 3 Вт / (м æ К), δ = 10 мм] составляет q = 3 æ 10 4 Вт / м 2 . Со стороны одной из ее поверхностей заданы температура жидкости
t ж = 30 °С и коэффициент теплоотдачи α = 100 Вт/(м 2 æ К). Найти температуры на обеих поверхностях стенки.
1.13. Чтобы уменьшить до заданного значения тепловые потери с поверхности промышленного теплообменника, решили закупить
тепловую изоляцию с λ′ из = 0,2 Вт/(м æ К). Оказалось, что на складе имеется изоляция, для которой λ из ″ = 0,1 Вт/(м æ К), но она на 50 %
дороже первой. Больше или меньше (и насколько) придется заплатить за вторую изоляцию?
Решение. Количество закупаемого материала прямо пропорционально толщине изоляционного слоя. Тепловые потери будут равны заданному значению,
если δ′ из ⁄ λ′ из = δ из ″ ⁄ λ из ″ . Толщина слоя изоляции во втором случае в два раза
меньше, чем в первом. При этом стоимость второй изоляции составляет 75 % стоимости первой.
Ответ. За вторую изоляцию нужно будет заплатить на 25 % меньше.
1.14. Температура внешней металлической поверхности сушильной камеры t с1 = 150 °С. Сушильная камера изолирована матами из

Ч а с т ь п е р в а я . ТЕПЛОПРОВОДНОСТЬ
минеральной стекловаты. Толщина мата δ = 60 мм. Температура воздуха в помещении t ж2 = 15 °С и коэффициент теплоотдачи α 2 =
= 10 Вт/(м 2 æ К). Найдите температуру наружной поверхности тепловой изоляции t с2 .
Решение. Для минеральной стекловаты λ = 0,052 + 0,00064t. Для нахождения t с2 можно воспользоваться равенством
λ / δ ( t с1 – t с2 ) = α 2 (t с2 – t ж2 ),
в котором λ = 0,052 + 0,00032(t с1 + t с2 ). Методом подбора находим t с1 ≈ 28 °С.
Ответ. Температура t с2 = 28 °С.
1.15. Определить необходимую мощность радиаторов отопления аудитории, если кладка ее наружной стены (L = 8 м, H = 4,5 м, δ = = 0,5 м) выполнена из красного кирпича на холодном растворе, а температуры поверхностей t с1 = 12 °С и t с2 = –15 °С. (Окна условно отсутствуют.)
Какова глубина промерзания стены?
Как изменится полученный результат с учетом того, что слои штукатурки на внутренней и внешней поверхностях стены δ ш.вн =
= δ ш.вш = 10 мм при других одинаковых условиях, если: а) штукатурка известковая; б) штукатурка цементно-песчаная?
1.16. Окно в аудитории имеет сдвоенные рамы с зазором между стеклами 60 мм. Вычислить тепловые потери через оконный проем 3×3 м без учета конвекции в зазоре и теплового излучения, если толщина стекол δ = 4 мм, а температуры их соответствующих поверхностей t с1 = 12 °С и t с4 = –15 °С.
1.17. Температура воздуха в аудитории t ж1 = 19,5 °С, а внешнего воздуха t ж2 = –18 °С. Вычислить тепловые потери из аудитории, если
наружная стена (L = 8 м, H = 4,5 м, δ = 0,5 м, окон нет) из кирпичной кладки, а коэффициенты теплоотдачи к ее внутренней поверхности
α 1 = 5,8 Вт/(м 2 æ К) и с ее внешней поверхности α 2 = 15 Вт/(м 2 æ К).
1.18. В плоском бытовом вертикальном масляном обогревателе
с габаритными размерами 0,7×0,7×0,025 м коэффициент теплоотдачи от масла к внутренней поверхности стальных стенок [δ = 1,5 мм,

Г л а в а п е р в а я . СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
λ = 24 Вт/(м æ К)] составляет 100 Вт/(м 2 æ К). Вычислить тепловой поток от обогревателя и температуры его стенок со стороны масла (t ж1 = 80 °С) и воздуха (t ж2 = 18 °С), если коэффициент теплоотдачи
к воздуху 8 Вт/(м 2 æ К).
1.19. Определить расход сухого насыщенного пара (р = 1,98 æ 10 5 Па)
в батарее парового отопления (F = 3 м 2 ) производственного помещения, если температура воздуха в нем поддерживается 20 °С. Коэффициент теплоотдачи с поверхности батареи к воздуху составляет
α воз = 9,5 Вт/(м 2 æ К), а теплоотдача со стороны конденсирующегося пара на три порядка больше, чем α воз . Конденсат не переохлаждается; термическим сопротивлением стенки батареи пренебречь.
1.20. Плоские стальные стенки [δ = 10 мм, λ = 40 Вт/(м æ К)] сушильной камеры, внутри которой поддерживается температура 120 °С, необходимо изолировать слоем шлаковой ваты так, чтобы температура его наружной поверхности составляла 30 °С.
Коэффициент теплоотдачи к внутренней поверхности стен камеры 20 Вт/(м 2 æ К), с наружной поверхности слоя изоляции к
окружающему воздуху (20 °С) — 10 Вт/(м 2 æ К). Определить толщину слоя ваты, если для нее λ в = 0,06 + 0,000145t Вт/(м æ К).
1.21. Стенка промышленной нагревательной печи состоит из трех слоев. Первый слой — плотный шамотный кирпич толщиной δ 1 = = 250 мм; второй слой — легковесный шамотный кирпич толщиной δ 2 = 500 мм. Максимальная температура в первом слое t с1 = 800 °С. Третий слой — тепловая изоляция (шлаковая вата). На внешней поверхности третьего слоя t с4 = 50 °С. Температура воздуха в поме-
щении t ж2 = 30 °С, а α 2 = 10 Вт/(м 2 æ К). Чему равна толщина слоя шлаковой ваты δ 3 ?
Решение. Для плотного шамотного кирпича λ 1 = 1,06 + 0,0008t; для легковесного шамотного кирпича λ 2 = 0,79 + 0,00035t; для шлаковой ваты λ 3 = 0,06 + + 0,000145t. Плотность теплового потока от поверхности изоляции к воздуху q = = 10(50 – 30) = 200 Вт/м 2 .

Ч а с т ь п е р в а я . ТЕПЛОПРОВОДНОСТЬ
Температуру t с2 в плоскости соприкосновения плотного и легковесного кирпичей найдем из уравнения
q = λ 1 / δ 1 (t c1 – t c2 ),
где λ 1 = 1,06 + 0,0004(t с1 + t с2 ).
Решая уравнение, получаем t с2 = 770 °С. Температуру t с3 находим из уравнения
q = λ 2 / δ 2 (t c2 – t c3 ), где λ 2 = 0,79 + 0,000175(t с2 + t с3 ).
Получаем: t с3 = 674 °С. Теперь имеем:
λ 3 = 0,06 + 0,0000725(t с3 + t с4 ) = 0,112 Вт/(м æ К); δ 3 = λ 2 /q (t c3 – t c4 ) = 0,35 м = 350 мм.
Ответ. Толщина слоя шлаковой ваты δ 3 = 350 мм.
1.22. Вычислить линейную плотность теплового потока через стенки змеевиков из труб (d 2 ×δ = 42×5 мм) жароупорной стали [ λ = = 16,5 Вт/(м æ К)], если температуры их внутренней и наружной поверхностей составляют 450 и 580 °С соответственно.
При каком значении радиуса этой трубы температура в стенке равна 500 °С?