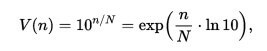Каждый ряд соответствует определённому допуску в номиналах деталей. Так, например компоненты из ряда E6 имеют допуск от номинала ±20 %, из ряда E12 — ±10 %, из E24 — ±5 %. Собственно, ряды устроены так, что следующее значение отличается от предыдущего чуть меньше, чем на двойной допуск. Значения номиналов для нескольких рядов приведены в таблице ниже.
Номинальные ряды деталей E3, E6, E12, E24
| E3 | E6 | E12 | E24 |
|---|---|---|---|
| 1,0 | 1,0 | 1,0 | 1,0 |
| 1,1 | |||
| 1,2 | 1,2 | ||
| 1,3 | |||
| 1,5 | 1,5 | 1,5 | |
| 1,6 | |||
| 1,8 | 1,8 | ||
| 2,0 | |||
| 2,2 | 2,2 | 2,2 | 2,2 |
| 2,4 | |||
| 2,7 | 2,7 | ||
| 3,0 | |||
| 3,3 | 3,3 | 3,3 | |
| 3,6 | |||
| 3,9 | 3,9 | ||
| 4,3 | |||
| 4,7 | 4,7 | 4,7 | 4,7 |
| 5,1 | |||
| 5,6 | 5,6 | ||
| 6,2 | |||
| 6,8 | 6,8 | 6,8 | |
| 7,5 | |||
| 8,2 | 8,2 | ||
| 9,1 |
Из таблицы становится понятно, что ряд E12 получается как-бы выкидыванием из ряда E24 каждого второго номинала, аналогичным образом получается, E6 вычёркиванием из E12.
Как видим в ряде E3 всего три члена: 1, 2.2, 4.7. Правда он в радиолюбительской практике не применяется. В E12 будет уже 12 членов: 1, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, 8.2
По своей сути номинальные ряды эта классическая таблица десятичных логарифмов или геометрическая прогрессия со знаменателем 10 1/n (для тех, кто в танке, математическая формула n-го члена геометрической прогрессии будет равна:
Выучив всего один раз ряд E24, можно, уме считать произведения чисел, корни небольших степеней, числовые логарифмы с точностью около ±5 %. Например, найдем квадратный корень из 1000. Десятичный логарифм 1000 равен 3, поделив его пополам, находим, что десятичный логарифм ответа 1,5 = 1 + 12/24, т. е. ответ есть 10 умноженное на множитель, стоящий в ряду E24 на 13-й позиции, т. е. точно в середине ряда, т. е. будет примерно 33.
Вычислить любой член ряда можно по формуле,

 |
 |
| Е48 | Е96 | Е192 | Е48 | Е96 | Е192 | Е48 | Е96 | Е192 | Е48 | Е96 | Е192 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 100 | 100 | 147 | 147 | 147 | 215 | 215 | 215 | 316 | 316 | 316 |
| 101 | 149 | 218 | 320 | ||||||||
| 102 | 102 | 150 | 150 | 221 | 221 | 324 | 324 | ||||
| 104 | 152 | 223 | 328 | ||||||||
| 105 | 105 | 105 | 154 | 154 | 154 | 226 | 226 | 226 | 332 | 332 | 332 |
| 106 | 156 | 229 | 336 | ||||||||
| 107 | 107 | 158 | 158 | 232 | 232 | 340 | 340 | ||||
| 109 | 160 | 234 | 344 | ||||||||
| 110 | 110 | 110 | 162 | 162 | 162 | 237 | 237 | 237 | 348 | 348 | 348 |
| 111 | 164 | 240 | 352 | ||||||||
| 113 | 113 | 165 | 165 | 243 | 243 | 357 | 357 | ||||
| 114 | 167 | 246 | 361 | ||||||||
| 115 | 115 | 115 | 169 | 169 | 169 | 249 | 249 | 249 | 365 | 365 | 365 |
| 117 | 172 | 252 | 370 | ||||||||
| 118 | 118 | 174 | 174 | 255 | 255 | 374 | 374 | ||||
| 120 | 176 | 258 | 379 | ||||||||
| 121 | 121 | 121 | 178 | 178 | 178 | 261 | 261 | 261 | 383 | 383 | 383 |
| 123 | 180 | 264 | 388 | ||||||||
| 124 | 124 | 182 | 182 | 267 | 267 | 392 | 392 | ||||
| 126 | 184 | 271 | 397 | ||||||||
| 127 | 127 | 127 | 187 | 187 | 187 | 274 | 274 | 274 | 402 | 402 | 402 |
| 129 | 189 | 277 | 407 | ||||||||
| 130 | 130 | 191 | 191 | 280 | 280 | 412 | 412 | ||||
| 132 | 193 | 284 | 417 | ||||||||
| 133 | 133 | 133 | 196 | 196 | 196 | 287 | 287 | 287 | 422 | 422 | 422 |
| 135 | 198 | 291 | 427 | ||||||||
| 137 | 200 | 200 | 294 | 294 | 432 | 432 | |||||
| 138 | 203 | 298 | 437 | ||||||||
| 140 | 140 | 140 | 205 | 205 | 205 | 301 | 301 | 301 | 442 | 442 | 442 |
| 142 | 208 | 305 | 448 | ||||||||
| 143 | 143 | 210 | 210 | 309 | 309 | 453 | 453 | ||||
| 145 | 213 | 312 | 459 |
 |
| E3 | E6 | E12 | E24 |
|---|---|---|---|
| 1,0 | 1,0 | 1,0 | 1,0 |
| 1,1 | |||
| 1,2 | 1,2 | ||
| 1,3 | |||
| 1,5 | 1,5 | 1,5 | |
| 1,6 | |||
| 1,8 | 1,8 | ||
| 2,0 | |||
| 2,2 | 2,2 | 2,2 | 2,2 |
| 2,4 | |||
| 2,7 | 2,7 | ||
| 3,0 | |||
| 3,3 | 3,3 | 3,3 | |
| 3,6 | |||
| 3,9 | 3,9 | ||
| 4,3 | |||
| 4,7 | 4,7 | 4,7 | 4,7 |
| 5,1 | |||
| 5,6 | 5,6 | ||
| 6,2 | |||
| 6,8 | 6,8 | 6,8 | |
| 7,5 | |||
| 8,2 | 8,2 | ||
| 9,1 |
Из таблицы становится понятно, что ряд E12 получается как-бы выкидыванием из ряда E24 каждого второго номинала, аналогичным образом получается, E6 вычёркиванием из E12.
Как видим в ряде E3 всего три члена: 1, 2.2, 4.7. Правда он в радиолюбительской практике не применяется. В E12 будет уже 12 членов: 1, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, 8.2
По своей сути номинальные ряды эта классическая таблица десятичных логарифмов или геометрическая прогрессия со знаменателем 10 1/n (для тех, кто в танке, математическая формула n-го члена геометрической прогрессии будет равна:
Выучив всего один раз ряд E24, можно, уме считать произведения чисел, корни небольших степеней, числовые логарифмы с точностью около ±5 %. Например, найдем квадратный корень из 1000. Десятичный логарифм 1000 равен 3, поделив его пополам, находим, что десятичный логарифм ответа 1,5 = 1 + 12/24, т. е. ответ есть 10 умноженное на множитель, стоящий в ряду E24 на 13-й позиции, т. е. точно в середине ряда, т. е. будет примерно 33.
Вычислить любой член ряда можно по формуле,

 |
 |
| Е48 | Е96 | Е192 | Е48 | Е96 | Е192 | Е48 | Е96 | Е192 | Е48 | Е96 | Е192 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 100 | 100 | 147 | 147 | 147 | 215 | 215 | 215 | 316 | 316 | 316 |
| 101 | 149 | 218 | 320 | ||||||||
| 102 | 102 | 150 | 150 | 221 | 221 | 324 | 324 | ||||
| 104 | 152 | 223 | 328 | ||||||||
| 105 | 105 | 105 | 154 | 154 | 154 | 226 | 226 | 226 | 332 | 332 | 332 |
| 106 | 156 | 229 | 336 | ||||||||
| 107 | 107 | 158 | 158 | 232 | 232 | 340 | 340 | ||||
| 109 | 160 | 234 | 344 | ||||||||
| 110 | 110 | 110 | 162 | 162 | 162 | 237 | 237 | 237 | 348 | 348 | 348 |
| 111 | 164 | 240 | 352 | ||||||||
| 113 | 113 | 165 | 165 | 243 | 243 | 357 | 357 | ||||
| 114 | 167 | 246 | 361 | ||||||||
| 115 | 115 | 115 | 169 | 169 | 169 | 249 | 249 | 249 | 365 | 365 | 365 |
| 117 | 172 | 252 | 370 | ||||||||
| 118 | 118 | 174 | 174 | 255 | 255 | 374 | 374 | ||||
| 120 | 176 | 258 | 379 | ||||||||
| 121 | 121 | 121 | 178 | 178 | 178 | 261 | 261 | 261 | 383 | 383 | 383 |
| 123 | 180 | 264 | 388 | ||||||||
| 124 | 124 | 182 | 182 | 267 | 267 | 392 | 392 | ||||
| 126 | 184 | 271 | 397 | ||||||||
| 127 | 127 | 127 | 187 | 187 | 187 | 274 | 274 | 274 | 402 | 402 | 402 |
| 129 | 189 | 277 | 407 | ||||||||
| 130 | 130 | 191 | 191 | 280 | 280 | 412 | 412 | ||||
| 132 | 193 | 284 | 417 | ||||||||
| 133 | 133 | 133 | 196 | 196 | 196 | 287 | 287 | 287 | 422 | 422 | 422 |
| 135 | 198 | 291 | 427 | ||||||||
| 137 | 200 | 200 | 294 | 294 | 432 | 432 | |||||
| 138 | 203 | 298 | 437 | ||||||||
| 140 | 140 | 140 | 205 | 205 | 205 | 301 | 301 | 301 | 442 | 442 | 442 |
| 142 | 208 | 305 | 448 | ||||||||
| 143 | 143 | 210 | 210 | 309 | 309 | 453 | 453 | ||||
| 145 | 213 | 312 | 459 |
 |
| Ряд | Допуск |
| E3 | ±50% |
| E6 | ±20% |
| E12 | ±10% |
| E24 | ±5% |
| E48 | ±2% |
| E96 | ±1% |
| E192 | ±0,5%, 0,25%, 0,1% и точнее |
Получается, что погрешность элементов, соответствующих величинам из E3, может отличаться в половину в обе стороны, тогда как у распространённого E24 всего лишь на 5 процентов. Рассмотрим типовые величины.
Для резисторов
На рынке можно найти сопротивления из всех существующих рядов, разве что E3 не встречаются в новых компонентах. В таблице ниже приведены значения для групп E3, E6, E12, E24, последние три встречаются чаще всего.
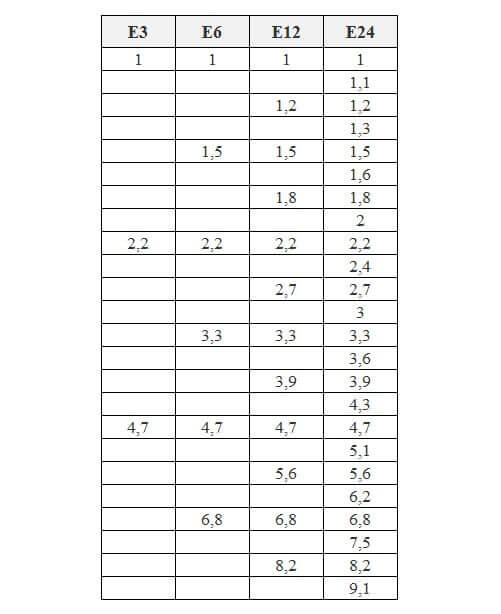
Также приводим величины из рядов номиналов E48, E96, E192.

Новички часто спрашивают: «Как пользоваться этими цифрами?»
Всё достаточно просто. Представим вы рассчитывали резистор для какой-то цепи. В результате получилось, что нужен элемент сопротивлением в 1170 Ом.
Проанализировав, какие можно купить в ближайшем магазине, решили, что нужно выбирать из объема значений E24 и увидели, что там есть числа 1,1 и 1,2. Эти числа нужно умножить или разделить на 10 столько раз, чтобы получилось приближенная к вашим расчетам величина, например:
Здесь 1200 Ом или 1,2 кОм ближе к 1170 Ом, чем 1,1 кОм. Значит вы уже выбрали подходящую величину из ряда номиналов E24. Таким образом вы можете подобрать соответствие расчетного резистора реальному, который сможете найти в продаже или у себя в закромах.

Для конденсаторов и индуктивности
С ёмкостью постоянных конденсаторов дело обстоит похожим образом. Но чаще всего встречаются в продаже элементы из рядов ЕЗ, Е6, Е12, Е24, реже Е48, Е96 и Е192. Это связано с тем, что конденсаторы с меньшим допуском изготовить сложно.

Способ использования приведённых выше таблиц аналогичен. Для примера ниже мы разместим таблицу с кодовым обозначением и номинальной ёмкостью конденсаторов из E3 и E6 в пико- нано- и микрофарадах.
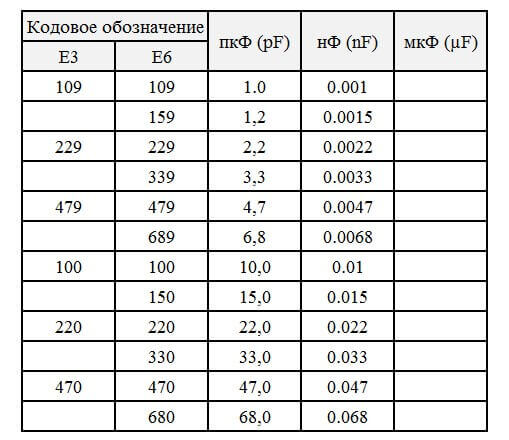
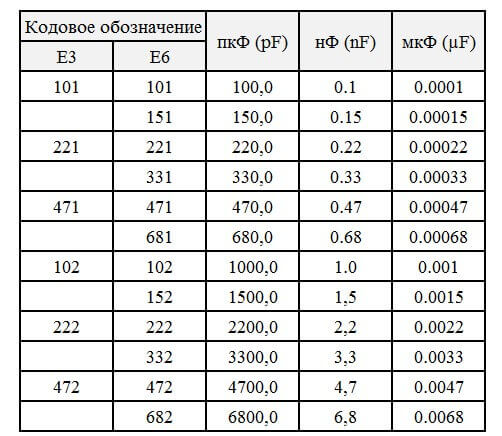
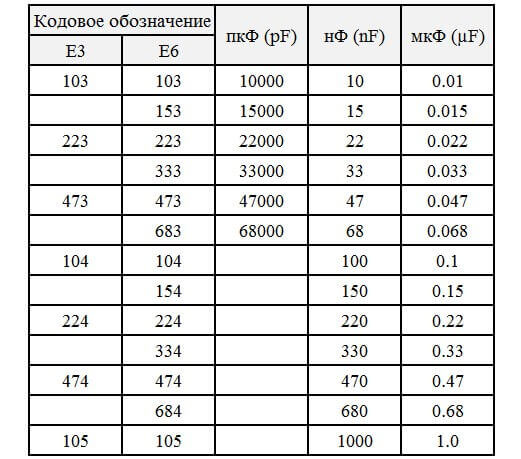
Катушки индуктивности или, как их еще называют, дроссели выпускаются производителями по тем же правилам – индуктивность чаще всего соответствуют значениям из Е12 или Е24.
Стоит отметить, что в большинстве электронных схем не требуется высокая точность выбора радиоэлектронных компонентов и отклонение в 5 и даже в 10% считается вполне допустимым. Тем более, купив несколько одинаковых деталей, вы можете измерить их реальное сопротивление, индуктивность или ёмкость и отобрать наиболее приближенные к расчетным. Также учитывайте особенности работы устройства, например, как изменяются номиналы элементов при разных температурах. Это и все, что мы хотели рассказать вам о том, какие бывают ряды номиналов радиодеталей.