Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнить арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.
Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
Алгоритм построения логических схем :
1) Определить число логических переменных.
2) Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей вентиль.
4) Соединить вентили в порядке выполнения логических операций.
Составить логическую схему для логического выражения: F = ¬ X v Y & X .
1) Две переменные – X и Y .
2) Две логические операции: 1 3 2
3) Строим схему, соединяя вентили в порядке выполнения логических операций:
Постройте логическую схему, соответствующую логическому выражению F = X & Y v ¬ ( Y v X ).
Вычислить значения выражения для X =1, Y =0.
1) Переменных две: X и Y .
2) Логических операций четыре: конъюнкция, две дизъюнкции и отрицание. Определяем порядок выполнения операций:
3) Схему строим слева направо в соответствии с порядком выполнения логических операций:
4) Вычислим значение выражения: F =1&0 v ¬ ( 0 v 1)=0.
Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения:
1) F=A v B& ¬ C, если A=1, B=1, C=1 .
2) F = ¬ (A v B&C), если A=0, B=1, C=1 .
3) F = ¬ A v B&C, если A=1, B=0, C=1 .
4) F =(A v B)&(C v B), если A=0, B=1, C=0 .
5) F = ¬ (A&B&C), если A=0, B=0, C=1 .
6) F=B& ¬ A v ¬ B&A, если A=0, B=0 .
7) F= ¬ (A&B&C) v (B&C v ¬ A), если A=1, B=1, C=0 .
И, ИЛИ, НЕ и их комбинации
В Булевой алгебре, на которой базируется вся цифровая техника, электронные элементы должны выполнять ряд определённых действий. Это так называемый логический базис. Вот три основных действия:
ИЛИ – логическое сложение (дизъюнкция) – OR;
И – логическое умножение (конъюнкция) – AND;
НЕ – логическое отрицание (инверсия) – NOT.
Примем за основу позитивную логику, где высокий уровень будет "1", а низкий уровень примем за "0". Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.
Логический элемент И.
На рисунке представлена таблица истинности элемента "И" с двумя входами. Хорошо видно, что логическая единица появляется на выходе элемента только при наличии единицы на первом входе и на втором. В трёх остальных случаях на выходе будут нули.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
На принципиальных схемах логический элемент "И" обозначают так.
На зарубежных схемах обозначение элемента "И" имеет другое начертание. Его кратко называют AND.
Логический элемент ИЛИ.
Элемент "ИЛИ" с двумя входами работает несколько по-другому. Достаточно логической единицы на первом входе или на втором как на выходе будет логическая единица. Две единицы так же дадут единицу на выходе.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
На схемах элемент "ИЛИ" изображают так.
На зарубежных схемах его изображают чуть по-другому и называют элементом OR.
Логический элемент НЕ.
Элемент, выполняющий функцию инверсии «НЕ» имеет один вход и один выход. Он меняет уровень сигнала на противоположный. Низкий потенциал на входе даёт высокий потенциал на выходе и наоборот.
| Вход X | Выход Y |
|---|---|
| 1 | |
| 1 |
Вот таким образом его показывают на схемах.
В зарубежной документации элемент "НЕ" изображают следующим образом. Сокращённо называют его NOT.
Все эти элементы в интегральных микросхемах могут объединяться в различных сочетаниях. Это элементы: И–НЕ, ИЛИ–НЕ, и более сложные конфигурации. Пришло время поговорить и о них.
Логический элемент 2И-НЕ.
Рассмотрим несколько реальных логических элементов на примере серии транзисторно-транзисторной логики (ТТЛ) К155 с малой степенью интеграции. На рисунке когда-то очень популярная микросхема К155ЛА3, которая содержит четыре независимых элемента 2И – НЕ. Кстати, с помощью её можно собрать простейший маячок на микросхеме.
Цифра всегда обозначает число входов логического элемента. В данном случае это двухвходовой элемент «И» выходной сигнал которого инвертируется. Инвертируется, это значит "0" превращается в "1", а "1" превращается в "0". Обратим внимание на кружочек на выходах – это символ инверсии. В той же серии существуют элементы 3И–НЕ, 4И–НЕ, что означает элементы «И» с различным числом входов (3, 4 и т.д.).
Как вы уже поняли, один элемент 2И-НЕ изображается вот так.
По сути это упрощённое изображение двух объёдинённых элементов: элемента 2И и элемента НЕ на выходе.
Зарубежное обозначение элемента И-НЕ (в данном случае 2И-НЕ). Называется NAND.
Таблица истинности для элемента 2И-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 1 | ||
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
В таблице истинности элемента 2И – НЕ мы видим, что благодаря инвертору получается картина противоположная элементу «И». В отличие от трёх нулей и одной единицы мы имеем три единицы и ноль. Элемент «И – НЕ» часто называют элементом Шеффера.
Логический элемент 2ИЛИ-НЕ.
Логический элемент 2ИЛИ – НЕ представлен в серии К155 микросхемой 155ЛЕ1. Она содержит в одном корпусе четыре независимых элемента. Таблица истинности так же отличается от схемы "ИЛИ" применением инвертирования выходного сигнала.
Таблица истинности для логического элемента 2ИЛИ-НЕ.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |
Изображение на схеме.
На зарубежный лад изображается так. Называют как NOR.
Мы имеем только один высокий потенциал на выходе, обусловленный подачей на оба входа одновременно низкого потенциала. Здесь, как и на любых других принципиальных схемах, кружочек на выходе подразумевает инвертирование сигнала. Так как схемы И – НЕ и ИЛИ – НЕ встречаются очень часто, то для каждой функции имеется своё условное обозначение. Функция И – НЕ обозначается значком "&", а функция ИЛИ – НЕ значком "1".
Для отдельного инвертора таблица истинности уже приведена выше. Можно добавить, что количество инверторов в одном корпусе может достигать шести.
Логический элемент "исключающее ИЛИ".
К числу базовых логических элементов принято относить элемент реализующий функцию «исключающее ИЛИ». Иначе эта функция называется «неравнозначность».
Высокий потенциал на выходе возникает только в том случае, если входные сигналы не равны. То есть на одном из входов должна быть единица, а на другом ноль. Если на выходе логического элемента имеется инвертор, то функция выполняется противоположная – «равнозначность». Высокий потенциал на выходе будет появляться при одинаковых сигналах на обоих входах.
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Эти логические элементы находят своё применение в сумматорах. «Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей "=1".
На зарубежный манер "исключающее ИЛИ" называют XOR и на схемах рисуют вот так.
Кроме вышеперечисленных логических элементов, которые выполняют базовые логические функции очень часто, используются элементы, объединённые в различных сочетаниях. Вот, например, К555ЛР4. Она называется очень серьёзно 2-4И-2ИЛИ-НЕ.
Её таблица истинности не приводится, так как микросхема не является базовым логическим элементом. Такие микросхемы выполняют специальные функции и бывают намного сложнее, чем приведённый пример. Так же в логический базис входят и простые элементы "И" и "ИЛИ". Но они используются гораздо реже. Может возникнуть вопрос, почему эта логика называется транзисторно-транзисторной.
Если посмотреть в справочной литературе схему, допустим, элемента 2И – НЕ из микросхемы К155ЛА3, то там можно увидеть несколько транзисторов и резисторов. На самом деле ни резисторов, ни диодов в этих микросхемах нет. На кристалл кремния через трафарет напыляются только транзисторы, а функции резисторов и диодов выполняют эмиттерные переходы транзисторов. Кроме того в ТТЛ логике широко используются многоэмиттерные транзисторы. Например, на входе элемента 4И стоит четырёхэмиттерный транзистор.
Схемотехническая реализация логических элементов. Построение логических схем.
В основе обработки компьютером информации лежит алгебра логики, разработанная Дж. Булем. Было доказано, что все электронные схемы ЭВМ могут быть реализованы с помощью логических элементов И, ИЛИ, НЕ.
При подаче на вход схемы сигнала низкого уровня (0) транзистор будет заперт, т.е. ток через него проходить не будет, и на выходе будет сигнал высокого уровня (1). Если же на вход схемы подать сигнал высокого уровня (1), то транзистор “откроется”, начнет пропускать электрический ток. На выходе за счет падения напряжения установится напряжение низкого уровня. Таким образом, схема преобразует сигналы одного уровня в другой, выполняя логическую функцию.
Функция “ИЛИ” — логическое сложение (дизъюнкция), ее результат равен 1, если хотя бы 1 из аргументов равен 1. Здесь транзисторы включены параллельно друг другу. Если оба закрыты, то их общее сопротивление велико и на выходе будет сигнал низкого уровня (логический “0”). Достаточно подать сигнал высокого уровня (“1”) на один из транзисторов, как схема начнет пропускать ток, и на сопротивлении нагрузки установится также сигнал высокого уровня (логическая “1”).
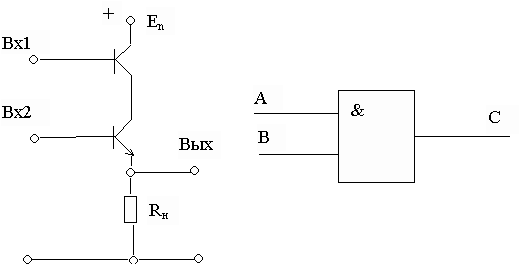
Если на входы Вх1 и Вх2 поданы сигналы низкого уровня (логические “0”), то оба транзистора закрыты, ток через них не проходит, выходное напряжение на Rн близко к нулю. Пусть на один из входов подано высокое напряжение (“1”). Тогда соответствующий транзистор откроется, однако другой останется закрытым, и ток через транзисторы и сопротивление проходить не будет. Следовательно, при подаче напряжения высокого уровня лишь на один из транзисторов, схема не переключается и на выходе остается напряжение низкого уровня. И лишь при одновременной подаче на входы сигналов высокого уровня (“1”) на выходе мы также получим сигнал высокого уровня.
Таким образом, каждой базовой логической функции – «И», «ИЛИ», «НЕ» — соответствует особым образом сконструированная схема, называемая логическим элементом. Комбинируя сигналы, обозначающие логические переменные, и выходы, соответствующие логическим функциям, с помощью логических элементов, пользуясь таблицей истинности или представлением логической функции в виде КНФ и ДНФ, можно составить структурную или функциональную схему (см. примеры ниже), являющуюся основой для аппаратной реализации схемы.
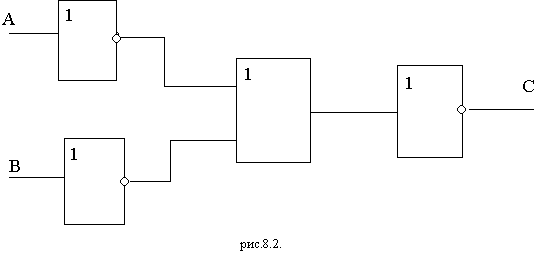
Анализируя функциональную схему, можно понять, как работает логическое устройство, т.е. дать ответ на вопрос: какую функцию она выполняет. Не менее важной формой описания логических устройств является структурная формула. Покажем на примере как выписывают формулу по заданной функциональной схеме (1 схема). Ясно, что элемент “И” осуществляет логическое умножение значений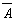 
и В. Над результатом в элементе “НЕ” осуществляется операция отрицания, т.е. вычисляется значение выражения: 
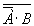Формула 
и есть структурная формула логического устройства.
Итак, основные логические функции обозначаются