Емкость батареи конденсаторов формула

Один из наиболее важных эффектов, используемых в электронике, — ёмкость конденсаторов. Способность накапливать и хранить электрический заряд нашла применение практически во всех аналоговых цепях и логических схемах. Пассивные устройства, запасающие энергию в виде электрического поля, называли конденсаторами уже в те времена, когда учёные ещё очень мало знали о природе электричества.

История накопителей заряда

Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.

Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.

Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.

Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:

• 1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
• 1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
• 1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
• конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
• начало XX в. — изобретение слюдяных и керамических конденсаторов.

Физика ёмкостных характеристик

Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.

Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.

Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.

Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:

• геометрия пластин;
• расстояние между ними;
• диэлектрический материал между пластинами.

Единица и формулы расчёта

Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.

Математическое выражение фарада

Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.

Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:

• пикофарад — 10—12 Ф;
• нанофарад — 10—9 Ф;
• микрофарад — 10—6 Ф.

Диэлектрическая проницаемость

Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:

• А — площадь меньшей пластины;
• d — расстояние между ними;
• ε — абсолютная проницаемость используемого диэлектрического материала.

Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.

На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:

Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.

Практические измерения

Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.

Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.

Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.

Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.

Идея суперконденсатора

Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.

Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:

• непродолжительный жизненный цикл;
• невысокая удельная мощность;
• узкий диапазон температур зарядки и разрядки;
• неспособность быстро отдать весь запас энергии.

Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.

Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.

Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.

1. батарея конденсаторов представляет собой два параллельно соединенных конденсаторов емкостями 3 и 6 мкФ. Определите емкость батареи

2. при условии последовательного соединения двух конденсаторов их общая емкость равна 1,2 мкФ. Емкость одного из конденсатора 2,0 мкФ. определите емкость второго конденсатора

• Попроси больше объяснений
• Следить
• Отметить нарушение

Nats3 12.09.2019

Что ты хочешь узнать?

Ответ

Объяснение:

1. батарея конденсаторов представляет собой два параллельно соединенных конденсаторов емкостями 3 и 6 мкФ. Определите емкость батареи

Сб = C1+C2 = 3 +6 = 9 мкФ

2. при условии последовательного соединения двух конденсаторов их общая емкость равна 1,2 мкФ. Емкость одного из конденсатора 2,0 мкФ. определите емкость второго конденсатора

Что такое электроемкость проводников

Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q 1 и q 2 ), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δ φ . Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U .

В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).

Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника ( q ) к разности потенциалов между этими двумя проводниками.

В виде формулы это записывается так: C = q ∆ φ = q U .

Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф .

Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.

Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.

Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.

Часть электрического поля вблизи конденсатора называется полем рассеяния.

Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.

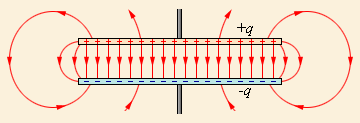
Рисунок 1 . 6 . 1 . Электрическое поле в плоском конденсаторе.

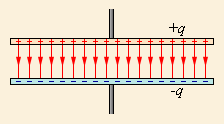
Рисунок 1 . 6 . 2 . Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.

Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:

Исходя из принципа суперпозиции, можно утверждать, что напряженность E → поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E + → и E — → полей каждой пластины, то есть E → = E + → + E — → .

Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E = 2 E 1 = σ ε 0 .

Как рассчитать электроемкость конденсатора

Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, E будет равно нулю. Если мы обозначим заряд каждой обкладки как q , а ее площадь как S , то соотношение q S даст нам представление о поверхностной плотности. Умножив E на расстояние между обкладками ( d ) , мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.

C = q ∆ φ = σ · S E · d = ε 0 S d .

Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.

Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.

Введем обозначение емкости в виде буквы С и запишем это в виде формулы:

Данная формула называется формулой электроемкости плоского конденсатора.

Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.

Сферическим конденсатором называется система из 2 -х концентрических сфер, сделанных из проводящего материала, радиусы которых равны R 1 и R 2 соответственно.

Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна L , а радиусы R 1 и R 2 .

Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:

• C = 4 πε 0 ε R 1 R 2 R 2 — R 1 (сферический конденсатор),
• C = 2 π ε 0 ε L ln R 2 R 1 (цилиндрический конденсатор).

Как рассчитать электроемкость батареи конденсаторов

Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.

Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: U 1 = U 2 = U , а заряды можно найти по формулам q 1 = С 1 U и q 2 = C 2 U . При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна C , заряд – q = q 1 + q 2 , а напряжение – U . В виде формулы это выглядит так:

С = q 1 + q 2 U или C = C 1 + C 2

Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.

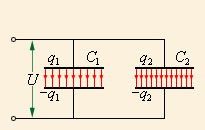
Рисунок 1 . 6 . 3 . Конденсаторы, соединенные параллельно. C = C 1 + C 2

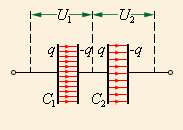
Рисунок 1 . 6 . 4 . Конденсаторы, соединенные последовательно: 1 C = 1 C 1 + 1 C 2

Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: q 1 = q 2 = q . Найти их напряжения можно так: U 1 = q C 1 и U 2 = q C 2 . Такую систему тоже можно считать одним конденсатором, заряд которого равен q , а напряжение U = U 1 + U 2 .

C = q U 1 + U 2 или 1 C = 1 C 1 + 1 C 2

Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.

Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.

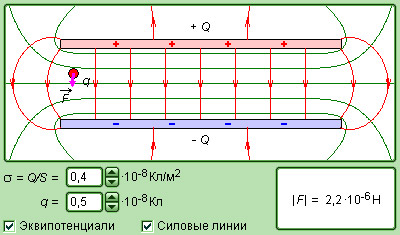
Рисунок 1 . 6 . 5 . Смоделированное электрическое поле плоского конденсатора.